Bias 와 Variance 간의 tradeoff 관계를 여러가지 관점에서 해석해보고자 한다.
용어
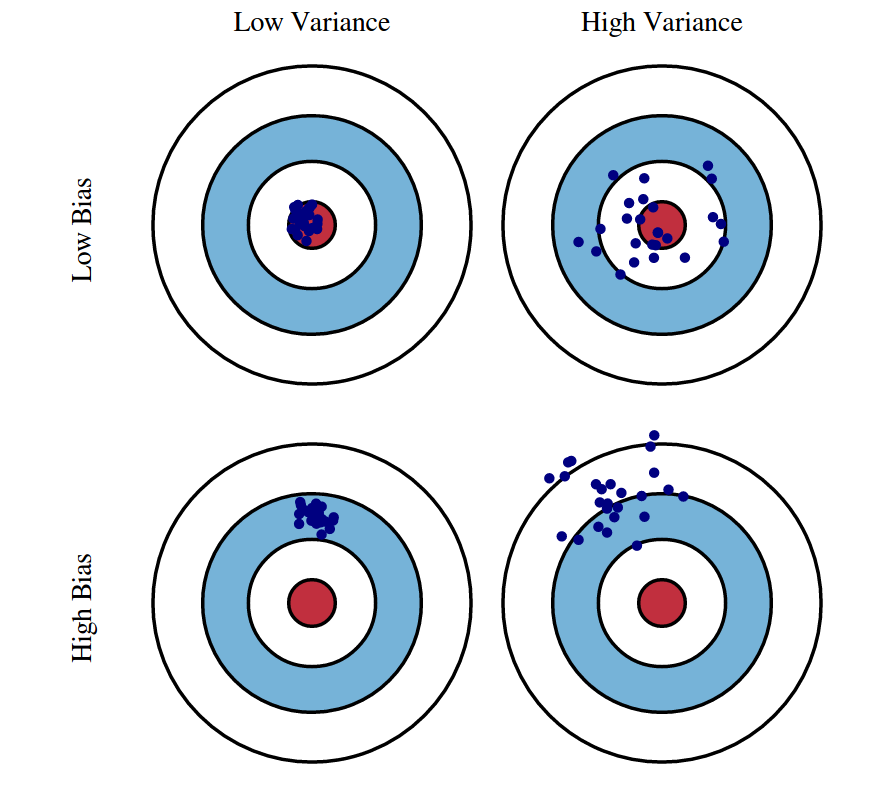
Bias (편향)
- Learning algorithm에서 잘못된 가정(assumption)을 했을 때 발생하는 오차(error)
- 높은 bias 는 쏠림,치우침(편향)이 심하다는 의미이며 underfitting 문제를 야기한다.
Variance (분산)
- Training set에 내재된 작은 변동(flucuation) 때문에 발생하는 오차(error)
- 높은 variance는 흩어져있다(큰 노이즈까지 모델링에 포함)는 의미이며 overfitting 문제를 야기한다.
Tradeoff (상충관계)
- 한 쪽에서 이득을 얻으면 다른 쪽은 손해를 얻는 관계
원본 : https://www.cs.cornell.edu/courses/cs4780/2018fa/lectures/lecturenote12.html
Lecture 12: Bias Variance Tradeoff
Lecture 12: Bias-Variance Tradeoff Video II As usual, we are given a dataset $D = \{(\mathbf{x}_1, y_1), \dots, (\mathbf{x}_n,y_n)\}$, drawn i.i.d. from some distribution $P(X,Y)$. Throughout this lecture we assume a regression setting, i.e. $y \in \mathbb
www.cs.cornell.edu
수식
다음과 같은 test error를 정의하는 식이 있다고 가정하자.
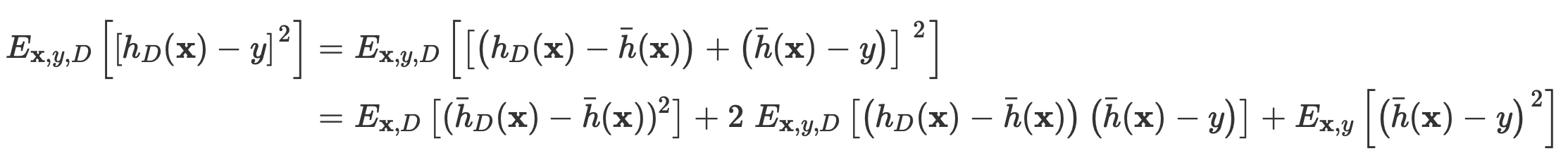
이때 다음과 같이 variance를 해석, 정의할 수 있다.
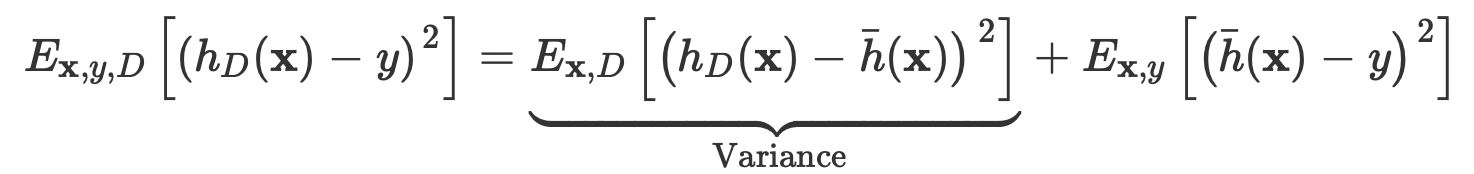
또한 처음 제시한 수식의 두번째 term을 보았을 때는 Noise와 Bias를 다음과 같이 해석할 수 있다.

추가로 첫 식을 약간만 전개하면 다음과 같은 결과를 얻는데

이를 조금 다르게 적용시키면

위와 같은 결과를 얻을 수 있고
결론적으로
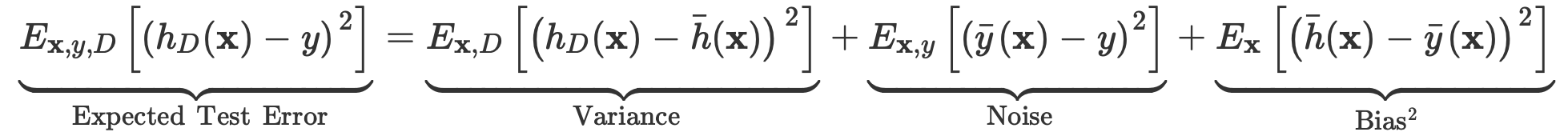
와 같은 test error에 대한 해석을 얻을 수 있다.
즉,
Expected Test Error 는 Variance, Noise , Bias로 구성된다고 볼 수 있다.
결론
수식을 말로 풀어서 표현하면 다음과 같이 표현할 수 있을 것 같다.
데이터를 표현하고자 하는 함수가 복잡할수록 더 많은 데이터를 포착할 수 있기 때문에 bias는 작아지지만, 그만큼 모델이 더 많이 움직이기 때문에 variance는 커지는 결과를 얻는다. vice-versa

원본 : https://towardsdatascience.com/bias-and-variance-but-what-are-they-really-ac539817e171
Bias and variance, but what are they really?
If you take a machine learning course, at some point you will encounter the bias-variance trade-off. You probably feel like you sort of…
towardsdatascience.com
'MACHINE LEARNING' 카테고리의 다른 글
| openCV / K-means clustering 시각화 (1) | 2023.03.15 |
|---|---|
| Approximate inference 정리 (0) | 2023.02.21 |
| Word2Vec 개념 정리 (0) | 2022.12.30 |
| ML / 3가지 주요 원칙 (2) | 2022.09.16 |
| NLP / Matching the Blanks: Distributional Similarity for Relation Learning 논문 요약 (0) | 2022.08.28 |