중심극한정리 : Central Limit Theorem
정의 vs 정리
이미 많이들 아시다시피 정의(Definition)과 정리(Theorem)은 서로 다른 개념이다.
정의(Definition)는 어떤 개념이나 용어의 의미를 정확히 정의(Define)하는 것이고
정리(Theorem)는 어떤 가설이나 명제를 증명(prove)하는 것이다.
가령, "집합"을 정의하기 위해 "원소"라는 개념을 사용하게되고, "집합은 서로 구별 가능한 원소들의 모임이다" 라는 정의를 사용해 "집합"을 정의한다.
반면, "만약 A가 B라면, A는 C이다"를 증명하고싶을 때, 적절한 수학적 기법과 논리를 사용하여 증명해야 한다. 아마 해당 가설은 삼단논법을 통해 매우 유명한 예시로 다들 알고있을 것이다.
중심극한정리는 통계학에서 매우 중요한 정리 중 하나이다.
해당 정리는 대부분의 독립적인 확률 변수들의 합이 정규 분포와 비슷한 분포를 따르게 된다는 것을 보여준다.
이때, 중심이란 용어는 분포의 중심이 정규 분포와 일치한다는 것을 의미하고, 극한(limit)은 샘플의 크기가 충분히 커질 때, 분포가 어떠한 분포에서도 일정한 방향으로 수렴한다는 것을 의미한다.
즉, 대부분의 독립적인 확률 변수들의 합이 정규 분포와 비슷한 분포를 따르게 되는 일반적인 규칙을 설명하는 정리이다.

정규분포(Normal distribution / Gaussian distribution)
중심극한정리는 정규분포와 관련이 깊다
사실, 정규분포 자체는 자연계 및 공학계열에서 매우 많은 현상을 설명하기에 매우 중요한 역할을 한다. 꽤나 많은 현상들이 실제로 이 분포를 따른다는 사실이 입증되어있기 때문이다.
정규분포에 대한 자세한 설명은 하지 않을 것이며 평균(mean)과 표준편차(Standard deviation)을 갖고, 대칭성이 특징인 분포의 한 종류이다.
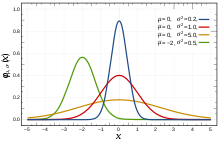
중심극한정리는 이러한 확률 변수들의 합이 정규 분포와 비슷한 분포를 따른다는 것을 보여준다.
즉, 독립적인 확률 변수들의 합이 정규분포의 특성인 "대칭성"과 "평균 주위의 집중성"을 따르게 됩니다.
위에서 간단히 언급한 수식을 예를 통해 해석해보자면 다음과 같다.
만약, 동전을 여러 번 던져서 나온 결과의 합을 계산해보면 결과값은 이항분포(binomial distribution)을 따르게 된다.하지만, 이항분포의 평균과 분산은 던진 횟수와 동전의 면이 나올 확률에 따라 달라지기 때문에, 이항 분포는 대부분 정규분포와 다른 모양을 띄게된다.하지만 중심극한정리에 따르면 , 동전을 여러 번 던지는 경우에도 결과값의 합이 충분히 크다면, 이 값은 정규분포와 비슷한 분포를 따르게 된다.
밑의 횟수에 따른 이항분포의 변화를 보면 이해가 직관적일 것이다.
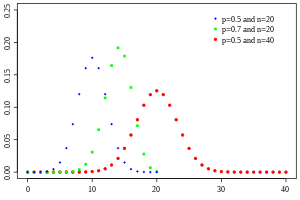
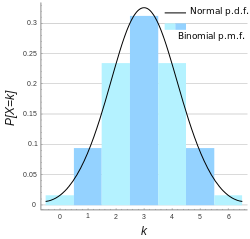

한계
중심극한정리를 통해 모집단(Population)의 평균과 표준편차를 추론(inference)할 수 있는 것이 해당 정리의 큰 목적 중 하나이다.
하지만, 중심극한정리를 사용하기 위해선 각 변수가 i.i.d 조건을 만족해야한다는 제약사항이 존재한다.
i.i.d 조건이란, independently Identically distributed 의 줄임말이다.
즉, 각 표본(sample)은 서로 독립적이고 동일한 분포를 가진다는 의미인데, 사실 통계학 대부분의 정리가 i.i.d 조건을 제약조건으로 하는 경우가 많기 때문에 특별한 상황이라고 볼 순 없지만 조건 자체를 성립해야한다는 점 자체는 변함이 없다.
'MACHINE LEARNING' 카테고리의 다른 글
| 논문 리뷰 / RAG VS FINE-TUNING: PIPELINES, TRADEOFFS, AND A CASESTUDY ON AGRICULTURE (0) | 2024.01.28 |
|---|---|
| OpenAI Assistant API 활용 예제 (Python Code) / ChatGPT (0) | 2023.11.12 |
| Degree of Freedom(자유도) 정리 (0) | 2023.04.09 |
| LDA / QDA 차이 비교 (0) | 2023.04.01 |
| 통계 / Chi-Squared distribution VS Poisson distribution (멍청일기) (0) | 2023.03.23 |