정의
Degree of Freedom(자유도) : 어떤 통계량이 자유롭게 변화할 수 있는 정도
자유도가 높을 수록 통계량의 변동성이 높아지며, 그만큼 더 정확한 추정치를 얻을 수 있다.
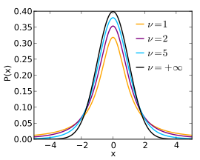
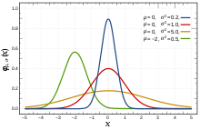
가령, t-distribution에서 자유도는 표본 크기와 관련이 있다.
표본 크기가 작으면 자유도가 작아지기 때문에 t-distribution의 꼬리(tail) 부분의 면적이 커지게되며 normal distribution과 달라지는 모습을 확인할 수 있다.
회귀(regression)에서도 자유도는 중요한 개념인데 SSE(Sum of Squared Error)나 SSR(Sum of Squared Residual)의 자유도는 각각 n-p-1과 p다.
(이때 p는 number of coefficient, 1은 intercept를 나타내기 위한 값이다.)
이 자유도는 추정된(estimated) 회귀계수(coefficient)의 수와 상수항(intercept) 등 모델 내의 자유도를 고려하여 결정하게 된다.
이를 통해 t-distribution을 이용한 가설 검정(Hypothesis test) 등의 통계적 추론(inference)가 가능해진다.
특징
자유도가 증가할수록 샘플의 변화가 더 자유롭게 가능하므로, 샘플의 분산(variance)이 커질 수 있다.
이는 추정치의 불확실성이 증가하게 되어 bias와 variance 사이의 trade-off가 발생하게 된다.
: bias 증가 시 variance 감소(flexibility 감소): bias 감소 시 variance 증가(flexibility 증가)

따라서, 자유도가 증가하면 variance는 커지지만, 적절한 자유도를 선택하면 bias와 variance 사이의 trade-off를 조절할 수 있으며, 이를 통해 정확한 추정치를 얻을 수 있다.
즉, 적절한 자유도를 선택하면 모델의 일반화 성능을 향상시킬 수 있다.
적용
Sample Mean (Degree of Freedom : N)
Sample variance (Degree of Freedom: N-1)
T-distribution (Degree of Freedom: n-1)
Residual Standard Error (Degree of Freedom: n-p-1)
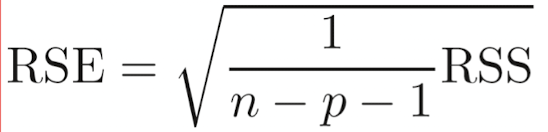
etc..
'MACHINE LEARNING' 카테고리의 다른 글
| OpenAI Assistant API 활용 예제 (Python Code) / ChatGPT (0) | 2023.11.12 |
|---|---|
| 중심극한정리 / Central Limit Theorem 에 대해 알아보자 (0) | 2023.04.22 |
| LDA / QDA 차이 비교 (0) | 2023.04.01 |
| 통계 / Chi-Squared distribution VS Poisson distribution (멍청일기) (0) | 2023.03.23 |
| openCV / image blur 처리 예제 (0) | 2023.03.15 |


